TLDR / Ce qu'il faut retenir de cette étude :
- Performance : +6,3 points de précision sur vos modèles avec seulement 30% de données collectées.
- Time-to-Market : Gain de 70% de temps, ici 691 jours de temps gagné sur la collecte et la labellisation.
- ROI Time-to-Market : donc 799 123€ sur 691 jours
- ROI récurrent de l’amélioration du modèle : 26 594 € / an
- ROI économie : 747 618 € d'économies générées en première année (moins de données à collecter) .
= On gagne 2 ans et > 800k€ et 26k€ par an et évitant de dépenser 747k€ dans la collecte de données.
Le dilemme de la Data Science : Imaginons un cas classique : vous devez entraîner un modèle pour détecter des transactions frauduleuses. Votre cible idéale ? 492 individus labellisés fraudeurs. Le problème ? La réalité du terrain. Chaque identification et validation d'un cas de fraude prend en moyenne 2 jours.
Ce délai met votre projet en péril. Attendre d'avoir 100% des données retarde la mise en production de l'algorithme et laisse votre entreprise vulnérable aux fraudes actuelles.
La question critique : Que se passe-t-il si l'on décide de développer le modèle plus vite, avec seulement 10%, 30% ou 50% des données ? → Traditionnellement, la robustesse du modèle s'effondre. Qui dit baisse de précision, dit fraudes non détectées et pertes financières sèches.
Mais existe-t-il une troisième voie ?
L’augmentation de données avec les données synthétiques
Cette voie, c'est l'augmentation de données. L'idée est simple et puissante : utiliser les données partielles déjà collectées (par exemple 30%) pour générer des données synthétiques (Avatars). Ces données sont statistiquement pertinentes et garantissent une anonymisation conforme au RGPD.
Analysons quantitativement l'impact de cette méthode sur un cas concret.
1. Performance : La puissance de l'augmentation
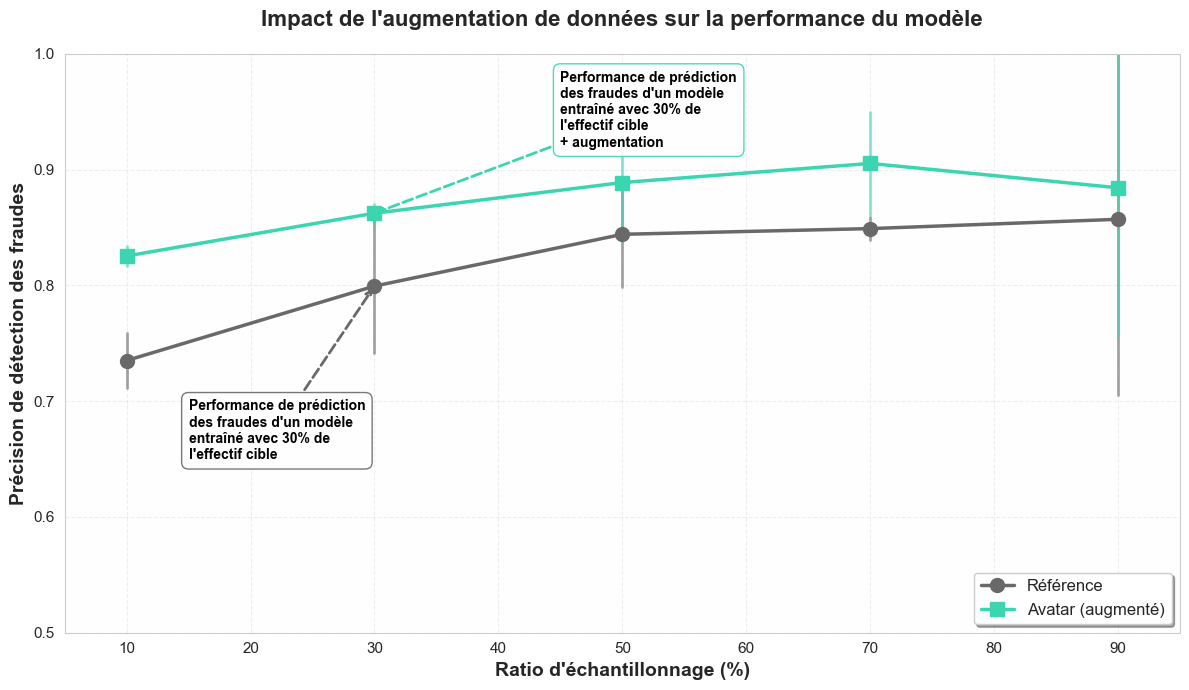
Le graphique ci-dessus illustre l'impact de l'augmentation de données sur la précision du modèle (métrique : Average Precision - métrique statistique correspondant au pourcentage de transactions frauduleuses qui sont bien détectées comme telles).
On observe une amélioration systématique de la performance lorsque les données sont augmentées avec Avatar (ligne verte), comparé à la méthode standard (ligne grise), et ce, quel que soit le volume de départ. Les barres d'erreur confirment que ce gain est statistiquement significatif.
Le chiffre à retenir : Avec seulement 30% des données réelles collectées, l'ajout de données synthétiques permet de bondir d'une précision de 79,9% à 86,2%.
Résultats :
- Un gain de +6,3 points de précision sans attendre la fin de la collecte.
En d’autres termes, sur mille transactions frauduleuses, le modèle entraîné avec des données augmentées en détectera 63 de plus. - Un gain de "Time to market" de 2 ans avec la mise sur le marché du produit de détection 2 ans plus tôt :
- 3454 fraudes par an à 122,21€ x 2 années
- = 844k€ de gain.
2. ROI Temporel : Une accélération majeure du projet
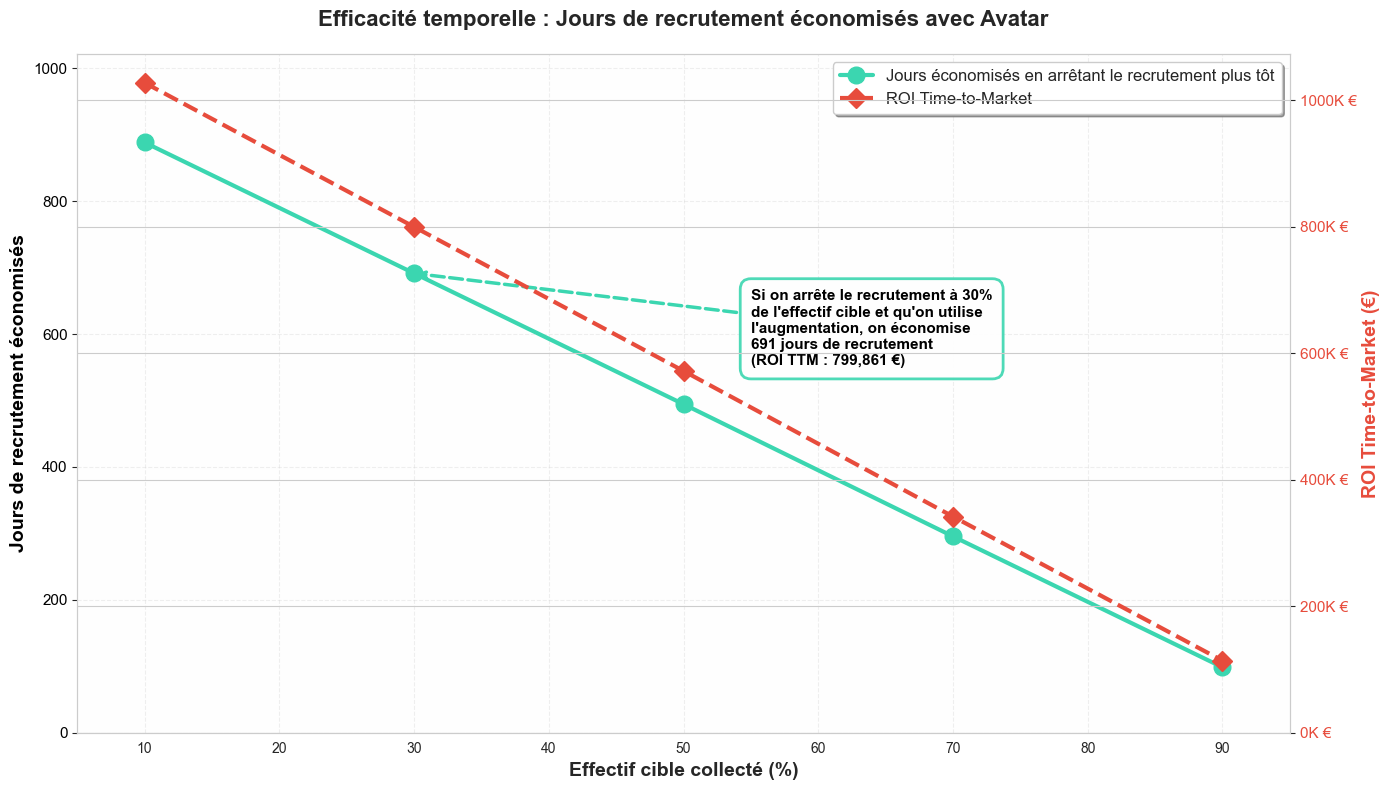
Le temps, c'est de l'argent, et le recrutement de données en demande beaucoup. Ce graphique viualise l’économie temporelle potentielle suite à l’utilisation d’une méthode d’augmentation.
La courbe verte représente le nombre de jours de "recrutement" (collecte/labellisation) économisés en arrêtant la collecte plus tôt et en compensant par de la donnée synthétique. Le temps de génération des données synthétiques étant négligeable (quelques minutes), le gain est significatif.
Le constat : Si vous arrêtez la collecte à 30% de l'objectif pour passer à l'augmentation :
👉 Vous économisez 691 jours de phase de collecte, contribuant à raccourcir le délai de mise en production de l’algorithme (Time-to-Market).
3. ROI Économique : La double économie
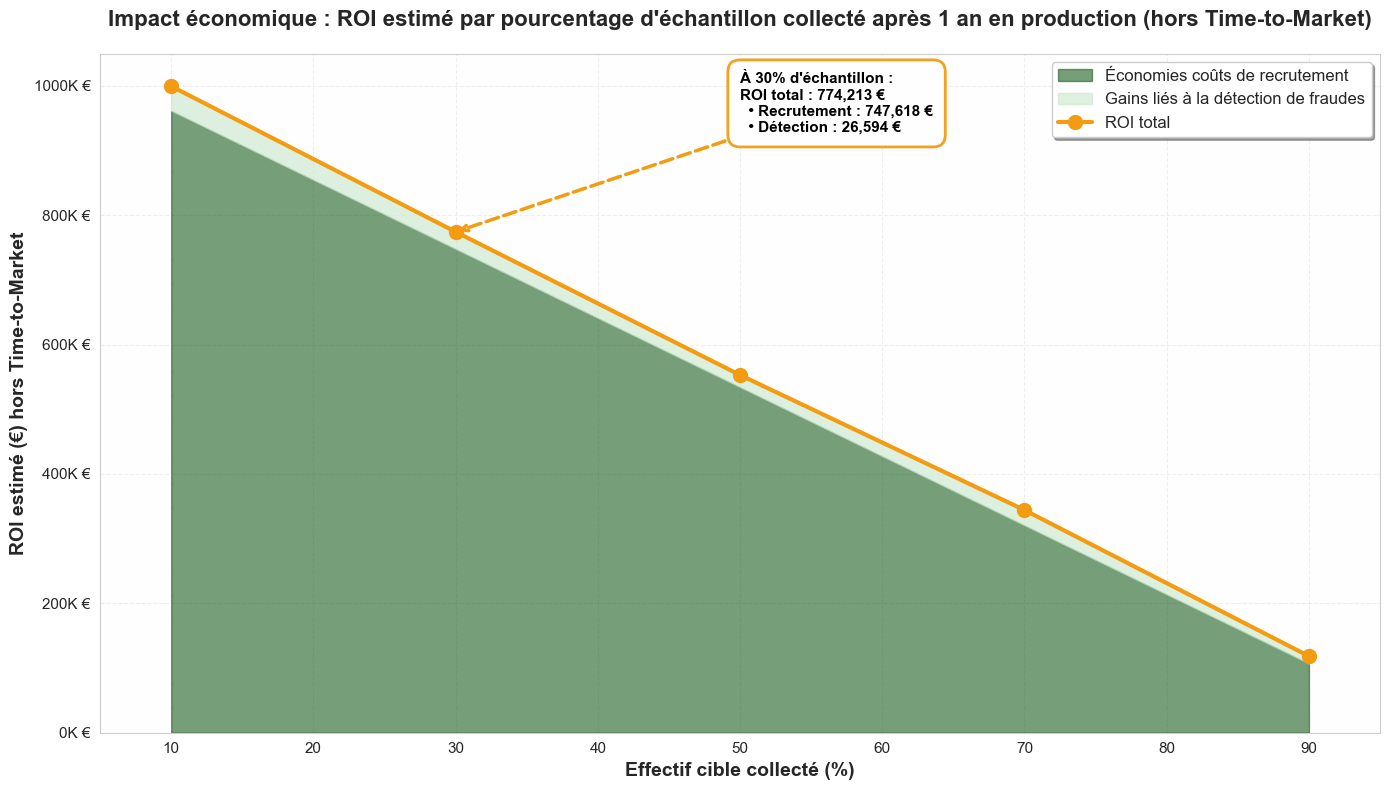
Le gain de temps s'accompagne mécaniquement d'une réduction des coûts. Mais l'économie est double :
- Coûts opérationnels : Moins de temps d'analyste/recruteur pour trouver et labelliser la donnée.
- Performance métier : Le modèle étant meilleur (voir point 1), il détecte plus de fraudes, réduisant les pertes.
L'impact chiffré (à 30% de collecte) : En arrêtant la collecte à 30% et en augmentant les données, l'économie totale estimée après 1 an de production s'élève à 774 213 €.
- Dont 747 618 € économisés sur le processus de recrutement/labellisation.
- Dont 26 594 € gagnés grâce à la meilleure détection des fraudes.
En résumé : La stratégie gagnante
Les résultats de l'expérimentation sont sans appel. Avec seulement 30% de données réelles complétées par des données synthétiques Avatar, vous obtenez :
- Une meilleure performance (+6.3 pts de précision).
- Une mise en production accélérée (691 jours de collecte évités).
- Un gain financier immédiat (~724k€ d'économies la première année).
- Une conformité RGPD totale (Privacy-by-design).
Conclusion : Vous obtenez un modèle plus performant, plus vite, et moins cher.
À VOUS DE JOUER
Ce cas d'usage sur la fraude bancaire est parfaitement transposable à d'autres secteurs critiques où la donnée est rare ou coûteuse à acquérir :
- Santé : recrutement de patients pour des essais cliniques.
- Banque/Assurance : analyse de sinistres atypiques.
- Industrie : détection de pannes spécifiques sur des chaînes de production.
- Administration : détection de fraude, paiements indus ou analyse prédictive de mesures d’économie.
- Défense : augmentation de la puissance statistique des données existantes
🔎 Annexe : Méthodologie et Hypothèses
Pour les profils techniques souhaitant reproduire ou comprendre le calcul, voici les paramètres de l'étude (basée sur le dataset creditcard et un modèle XGBoost).
Paramètres clés :
$$
\begin{array}{|c|l|r|}
\hline
\textbf{Symbole} & \textbf{Description} & \textbf{Valeur} \\
\hline
r & \text{Ratio d'échantillonnage (fraction de la cible collectée)} & \mathbf{30\%} \\
\hline
PTF & \text{Pourcentage de transactions frauduleuses} & \mathbf{0,1727\%}^\ast \\
\hline
NTA & \text{Nombre de transactions annuelles} & \mathbf{2\,000\,000} \\
\hline
NFA & \text{Nombre de fraudes annuelles } (PTF \times NTA) & \mathbf{3\,454} \\
\hline
CMTF & \text{Coût moyen par transaction frauduleuse} & \mathbf{122,21\,\text{€}}^\ast \\
\hline
CHA & \text{Coût horaire analyste} & \mathbf{45\,\text{€/h}} \\
\hline
TLD & \text{Temps de labellisation par donnée} & \mathbf{5\,\text{min}} \\
\hline
TAFL & \text{Temps acquisition fraude labellisée } (TLD/PTF) & \mathbf{2\,895,6\,\text{min}} \\
\hline
EF & \text{Échantillons de fraudes} & \mathbf{492} \\
\hline
TT & \text{Transactions totales} & \mathbf{284\,807} \\
\hline
\end{array}
$$
* Valeur calculée à partir des données
Formule de calcul des économies :
- 691 = 0.7 * 492 (économie de 70 % du recrutement cible) * (TAFL/60/24)
- 691 = 0.7 * 492 * (2895.6/60/24)
- 799 124 = CMTF * (NFA / 365) * 691
- 799 124 = 122.21 * (3454 / 365) * 691
- 26 594 = NFA * CMTF * 0.063 (augmentation de la perf du modèle)
- 26 594 = 3454 * 122.21 * 0.063
- 747618 = 0.7 * 492 (économie de 70 % du recrutement cible) * (TAFL / 60) * CHA
- 747618 = 0.7 * 492 * (2895.6 / 60) * 45
$$\boxed{\text{Économies}_{\text{Totales}}(r) = \text{Économies}_{\text{Recrutement}}(r) + \text{Économies}_{\text{Détection}}(r)}$$
où :
- $\text{Économies}_{\text{Recrutement}}(r) = \frac{(100 - r) \times \text{TAFL}}{60} \times \text{CHA}$ sont les économies liées à la réduction du temps de recrutement et labellisation ;
- $\text{Économies}_{\text{Détection}}(r) = \Delta\text{Précision}(r) \times \text{CMTF} \times \text{NFA}$ sont les économies liées à l'amélioration de la détection des fraudes.
Note : $\Delta\text{Précision}(r) = \text{Précision avec augmentation Avatar} - \text{Précision de référence}$
Pour en savoir plus :
🔗 Documentation : docs.octopize.io
📅 Calculez votre ROI potentiel avec nos experts : https://meeting.octopize.io/meetings/gabrielle-crolard/ai-diagnostic
📧 Contact : contact@octopize.io




.png)



