TLDR/What to remember from this study:
- Performance: +6.3 points accuracy on your models with only 30% of data collected.
- Time-to-market: Save 70% of time, here 691 days of time saved on collection and labelling.
- KING Time-to-market: therefore €799,123 over 691 days
- Recurring ROI from model improvement: €26,594/year
- Economic ROI: 747,618€ savings generated in the first year (less data to collect)
= We save 2 years and > 800k € and 26k € per year and avoid spending 747k € on data collection.
The Data Science Dilemma: Let's imagine a classic case: you need to train a model to detect fraudulent transactions. Your ideal target? 492 individuals labelled fraudsters. The problem? The reality on the ground. Each identification and validation of a fraud case takes on average 2 days.
This delay puts your project at risk. Waiting for 100% of the data delays the launch of the algorithm and leaves your company vulnerable to current fraud.
The critical question: What happens if you decide to develop the model faster, with only 10%, 30%, or 50% of the data? → Traditionally, the Model robustness collapses. Who says reduced precision, says undetected fraud and dry financial losses.
But is there a third way?
Increasing data with synthetic data
This path is data increase. The idea is simple and powerful: use the partial data already collected (for example 30%) to generate synthetic data (Avatars). These data are statistically relevant and guarantee a anonymization in accordance with the GDPR.
Let's analyze quantitatively the impact of this method on a concrete case.
1. Performance: The power of augmentation
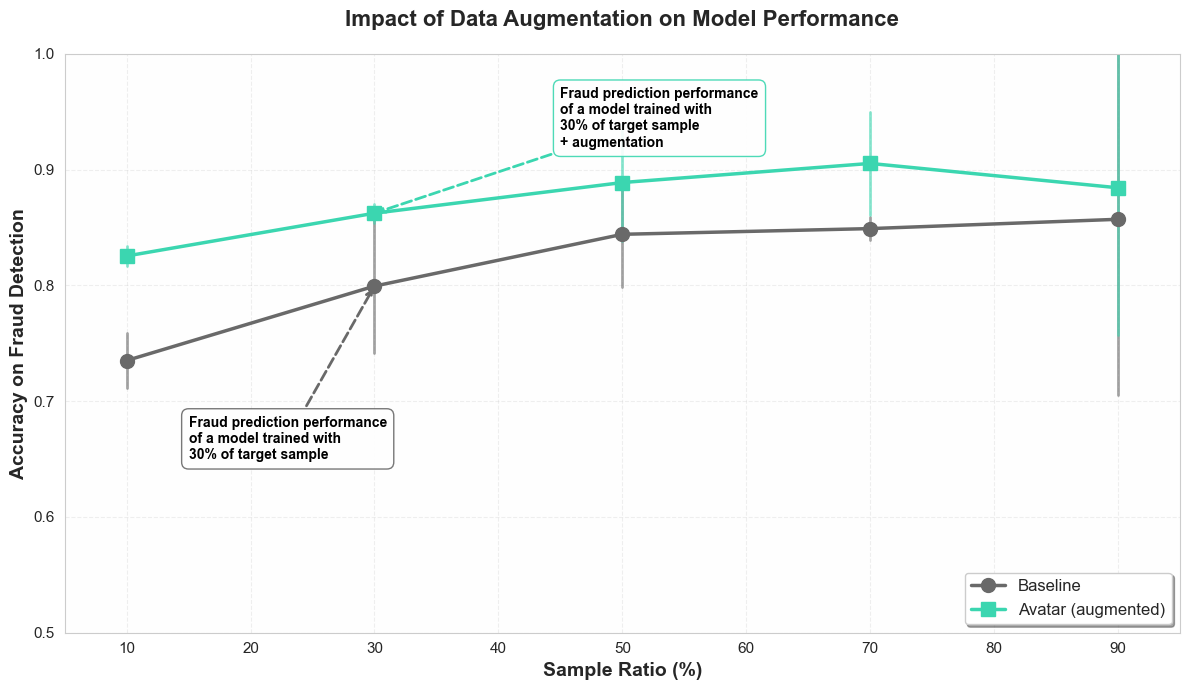
The graph above illustrates the impact of increased data on the accuracy of the model (metric: Average Precision - statistical metric corresponding to the percentage of fraudulent transactions that are well detected as such).
We observe a systematic improvement performance when the data is increased with Avatar (green line), compared to the standard method (gray line), regardless of the starting volume. The error bars confirm that this gain is statistically significant.
The number to remember : With only 30% of real data collected, the addition of synthetic data makes it possible to jump from an accuracy of 79.9% to 86.2%.
Results:
- A gain of +6.3 accuracy points without waiting for the end of the collection.
In other words, out of a thousand fraudulent transactions, the model trained with augmented data will detect 63 more. - A gain in “Time to market” of 2 years with the marketing of the detection product 2 years earlier:
- 3454 frauds per year at €122.21 x 2 years
- = 844k € of gain.
2. Temporal ROI: A major acceleration of the project
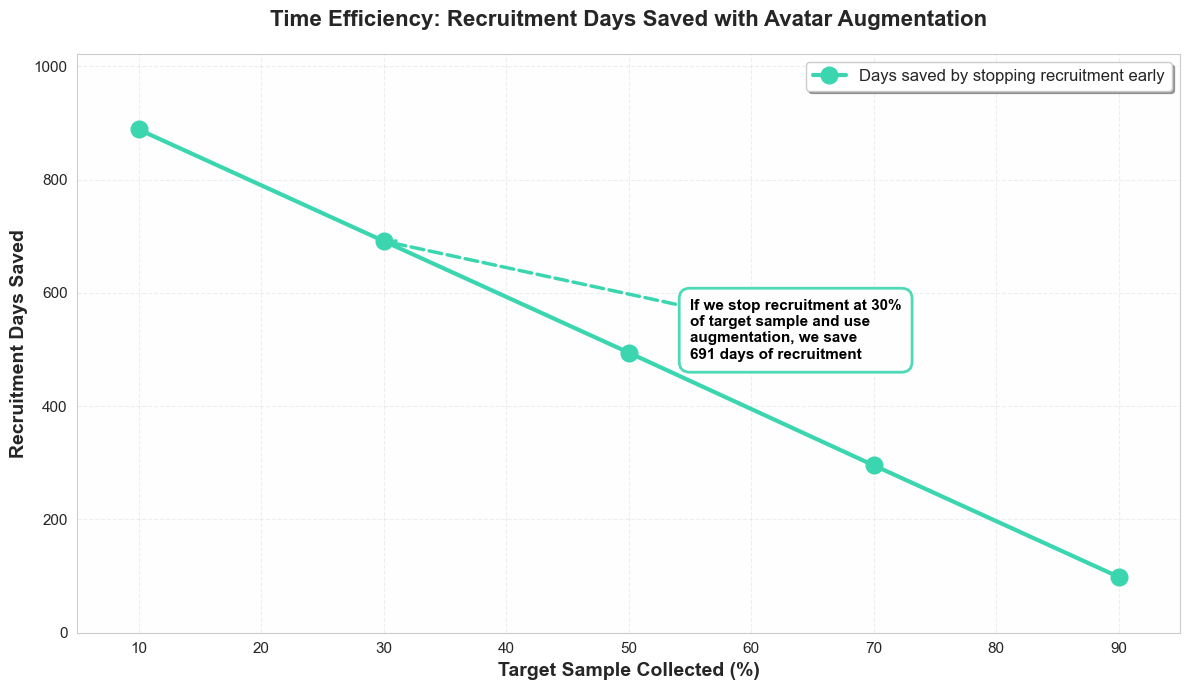
Time is money, and recruiting data requires a lot of time. This graph shows the potential time savings resulting from the use of an augmentation method.
The green curve represents the number of “recruitment” days (collection/certification) saved by stopping the collection earlier and compensating with synthetic data. Since the time to generate synthetic data is negligible (a few minutes), the gain is significant.
The observation : If you stop collecting at 30% of the goal to move on to the increase:
👉 You save 691 days of the collection phase, helping to shorten the time needed to put the algorithm into production (Time-to-Market).
3. Economic ROI: The dual economy
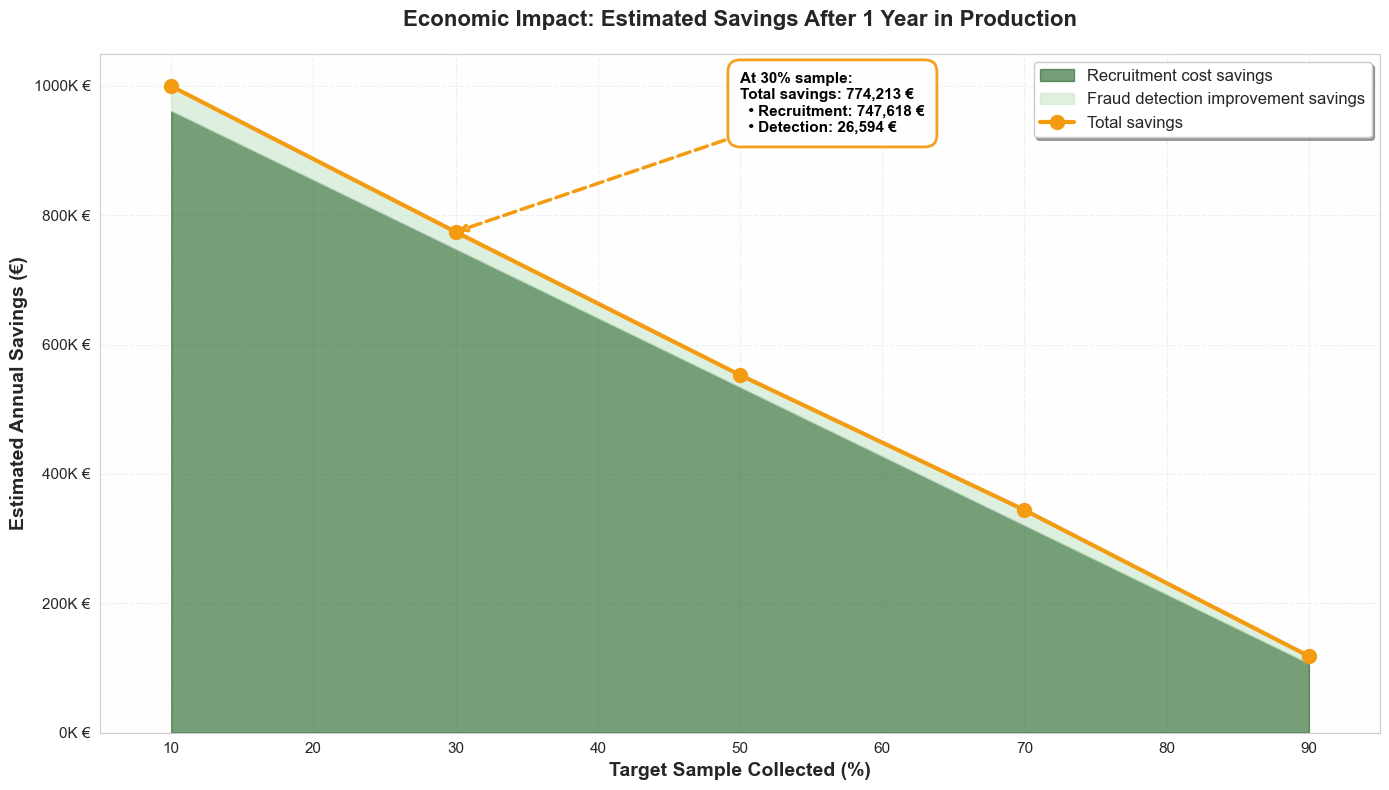
The saving of time is mechanically accompanied by a reduction in costs. But the economy is twofold:
- Operational costs: Less analyst/recruiter time to find and label data.
- Business performance: Since the model is better (see point 1), it detects more fraud, reducing losses.
The numerical impact (at 30% of collection) : By stopping the collection at 30% and increasing the data, the estimated total savings after 1 year of production amounts to 74,213€.
- Dont 747,618€ saved on the recruitment/certification process.
- Dont €26,594 won thanks to better fraud detection.
In summary: The winning strategy
The results of the experiment are unquestionable. With only 30% real data supplemented with Avatar synthetic data, you get:
- Better performance (+6.3 points of accuracy).
- Accelerated production (691 collection days avoided).
- Immediate financial gain (~€724k in savings the first year).
- RGPD compliance total (privacy-by-design).
Conclusion : You get a more efficient, faster, and cheaper model.
IT'S UP TO YOU TO PLAY
This use case on bank fraud is perfectly transposable to other critical sectors where data is rare or expensive to acquire:
- Health : recruitment of patients for clinical trials.
- Banking/Insurance : analysis of atypical claims.
- Industry : detection of specific failures on production lines.
- Administration : detection of fraud, undue payments or predictive analysis of savings measures.
- Defense : increasing the statistical power of existing data
🔎 Appendix: Methodology and Assumptions
For technical profiles wishing to reproduce or understand the calculation, here are the parameters of the study (based on the dataset): Credit card and an XGBoost model).
Key parameters:
$$
\begin{array}{|c|l|r|}
\hline
\textbf{Symbol} & \textbf{Description} & \textbf{Value} \\
\hline
r & \text{Sampling ratio (fraction of the target collected)} & \mathbf{30\%} \\
\hline
PTF & \text{Percentage of fraudulent transactions} & \mathbf{0.1727\%}^\ast \\
\hline
NTA & \text{Annual number of transactions} & \mathbf{2,000,000} \\
\hline
NFA & \text{Annual number of frauds } (PTF \times NTA) & \mathbf{3,454} \\
\hline
CMTF & \text{Average cost per fraudulent transaction} & \mathbf{122.21\,\text{€}}^\ast \\
\hline
CHA & \text{Analyst hourly rate} & \mathbf{45\,\text{€/h}} \\
\hline
TLD & \text{Labeling time per data point} & \mathbf{5\,\text{min}} \\
\hline
TAFL & \text{Acquisition time per labeled fraud } (TLD/PTF) & \mathbf{2,895.6\,\text{min}} \\
\hline
EF & \text{Fraud samples} & \mathbf{492} \\
\hline
TT & \text{Total transactions} & \mathbf{284,807} \\
\hline
\end{array}
$$
* Value calculated based on data
Formula for calculating savings:
- 691 = 0.7 * 492 (saving 70% of target recruitment) * (TAFL/60/24)
- 691 = 0.7 * 492 * (2895.6/60/24)
- 799,124 = CMTF * (NFA/365) * 691
- 799,124 = 122.21 * (3454/365) * 691
- 26 594 = NFA * CMTF * 0.063 (increased model performance)
- 26,594 = 3454 * 122.21 * 0.063
- 747618 = 0.7 * 492 (saving 70% of target recruitment) * (TAFL/60) * CHA
- 747618 = 0.7 * 492 * (2895.6/60) * 45
$$\boxed{\text{Savings}_{\text{Total}}(r) = \text{Savings}_{\text{Recruitment}}(r) + \text{Savings}_{\text{Detection}}(r)}$$
où :
- $\text{Savings}_{\text{Recruitment}}(r) = \frac{(100 - r) \times \text{TAFL}}{60} \times \text{CHA}$ represents the savings from reduced recruitment and labeling time ;
- $\text{Savings}_{\text{Detection}}(r) = \Delta\text{Precision}(r) \times \text{CMTF} \times \text{NFA}$ represents the savings from improved fraud detection.
Note : $\Delta\text{Precision}(r) = \text{Precision with Avatar augmentation} - \text{Baseline Precision}$
For more information:
🔗 Documentation : docs.octopize.io
📅 Calculate your Potential ROI with our experts: https://meeting.octopize.io/meetings/gabrielle-crolard/ai-diagnostic
📧 Contact : contact@octopize.io




.png)



